演算法系列：Directed Acyclic Graph

Directed Acyclic Graph 中文翻譯為：有向無環圖。文章通篇會來解釋關於 DAG 這個演算法。 但要談 DAG 演算法之前需要先認識幾個資料結構的知識：

• 什麼是 Graph?
• Graph 的種類
• Graph 地表示方式

什麼是 Graph?

Graph 稱為圖，是一種比 tree 更廣義的資料結構，當然也可以說 tree 是一種特殊的 Graph，它的組成是由點(vertex)和邊(edge)所構成。點和點之間透過邊來連接，相連得兩點代表有關聯性。

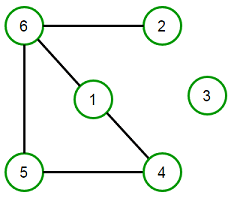
從圖來看，點和邊分別是：

• V(vertex):{1,2,3,4,5,6}
• E(edge):{(1,4),(1,6),(2,6),(4,5),(5,6)}

Graph 種類

接下來簡單介紹一下各種 Graph 包含我們會提到的 DAG (假設有 m 個 edges 和 n 個 vertex)。

Undirected graph

無向圖，顧名思義就是邊(edge)是沒有方向性的。因此 edge(x,y) 等同於 edge(y,x)。不是成對排序，最大的邊數 = n(n-1)/2

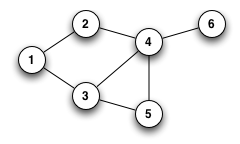
undirected, then m = n(n-1)/2

Directed graph(di-graph)

中文稱作，有向圖。有向圖指的是邊(edge) 有方向性，意思就是 edge(x,y) 定義上和 edge(y,x) 是不同的。

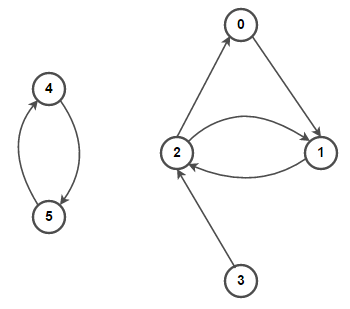
directed, then m = n(n-1)

Directed Acyclic Graph (DAG)

有向循環圖就是有向圖但是沒有循環(cycles)

Multigraph

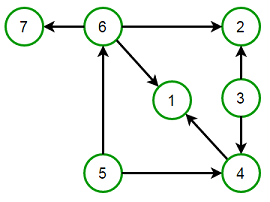
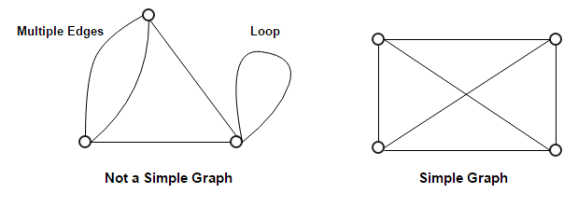
多圖是一個無向圖，允許多個邊 (可能有循環)。多邊意思是指兩個或以上的邊連接到兩個點，可以連結自身。

Simple graph

簡單圖不是多圖，是一個無向圖，不允許多個邊和循環。在簡單圖中有 n 個點，每個點最大自由度是 n-1

Weighted and Unweighted graph

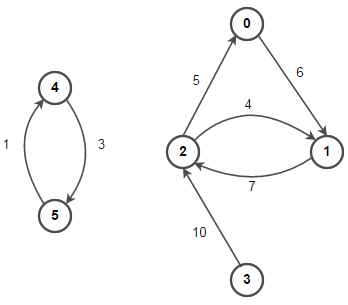
加權圖和沒有加權圖差異在是否賦予一個加權值給邊(edge)。

Complete graph

每個相鄰兩邊都都存在。

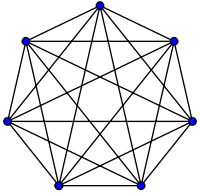
complete, then m = n(n-1)/2

Connected graph

每個點都需要是成對的邊，意思是指沒有到不了的點。因此 disconnected grapn 就是指都未連接。

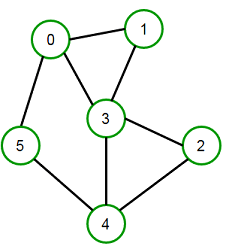
connected, then m = n – 1

Graph 地表示方式

在程式裡我們可以將這些有限的點與邊放進矩陣(matrix)內表示，在電腦則用陣列(array)存放。但用陣列存放卻不容易計算，因此有了幾種方法:

• adjacency matrix
• adjacency lists
• adjacency